放物線は1つだけ

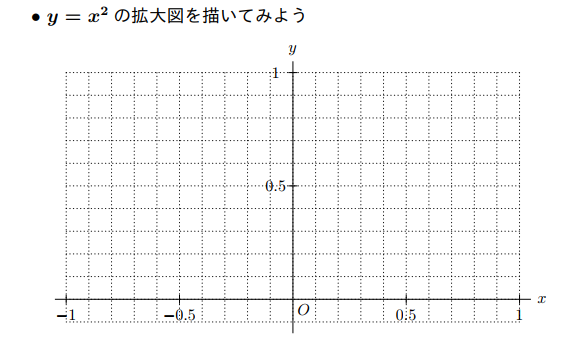
東書の教科書には上の課題が採用されている。
のグラフを1目盛1で描かせると、どうしても頂点が尖ってしまうので良い問題というか必須の問題だ。

ついでに次の課題もやったらどうか？

タイミングとしては、2乗比例のグラフの特徴をおさえて、比例定数の値によるグラフの形の変化をおさえた後あたりか。

こんな写真を見せて、これ全部 なんだよ。どれもだけど。

でも、実は放物線は円と同じで1つしかない...と展開したらちょっとした驚きになるのではないかな。

以前は2年生で相似を学んでいたのが、今は3年の関数の後になってしまったのが痛い。

証明

上の点に対し、
上の点を対応させる。
との座標の比も、座標の比も

なので、3点は一直線上に並ぶ。*1

*1:内項を入れ替えれば、OAの傾きとOBの傾きが等しいことがわかる。 もちろん相似比は 。